The microstructure of many materials is essentially disordered, meaning that there are a large number of small-scale structural elements which can be arranged in many possible ways. For instance, common metals, such as aluminum and nickel, are composed of a jumble of crystalline grains. Atoms within the crystalline grain are themselves ordered, but atoms at a grain boundary, where most deformation originates, occupy seemingly random positions. The mechanics of these disordered materials is one of the most famous open problems in materials physics.
Machine learning algorithms can help cut through the structural complexity [1,2,3]. The local structure can be projected down from the high-dimensional configuration space to a subspace of a single dimension which is highly-correlated with the susceptibility of the local region to deform. Then regions of weak structures can be readily identified so that the spatial distribution of weak spots can be connected to the origins of the material mechanical properties. The machine learning method can also be reverse engineered to expose the attributes that contribute to the weakness of a region. Furthermore, by looking for an Arrhenius relationship between temperature likelihood to deform, it is sometimes possible to identify the energy barrier associated with each small-scale deformation.
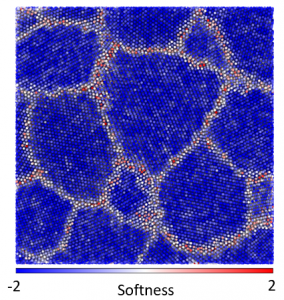
In previous work, I adapted and applied the above method, using a support vector machine, to study poly-crystalline materials. Typically, defects (dislocations, vacancies, grain boundaries…) are said to control the mechanics of these materials, but the disordered regions within the core of the defects affects the mechanics of the defects themselves. Our work demonstrated the dominant role of local structure in determining the weak spots within defects, even with realistic (delocalized) metallic bonding. In this material, a lack of symmetry of the atomic environment was responsible for weakening an area of the material. Contrary to expectations, though consistent with experimental measurements, the weak regions all had essentially the same energy barrier height preventing deformation. The work helped illuminate the connection between disordered regions within poly-crystals and bulk glasses.
[1] Cubuk, Ekin Dogus, Samuel Stern Schoenholz, Jennifer M. Rieser, Brad Dean Malone, Joerg Rottler, Douglas J. Durian, Efthimios Kaxiras, and Andrea J. Liu. “Identifying structural flow defects in disordered solids using machine-learning methods.” Physical review letters 114, no. 10 (2015): 108001.
[2] Schoenholz, Samuel S., Ekin D. Cubuk, Daniel M. Sussman, Efthimios Kaxiras, and Andrea J. Liu. “A structural approach to relaxation in glassy liquids.” Nature Physics 12, no. 5 (2016): 469-471.
[3] Sharp, Tristan A., Spencer Thomas, Ekin Dogus Cubuk, Samuel S. Schoenholz, David Srolovitz, Andrea J. Liu. “Using machine learning to extract atomic energy barriers in poly-crystalline materials.” Submitted 2017. Accepted PNAS 2018.
