Category: computing

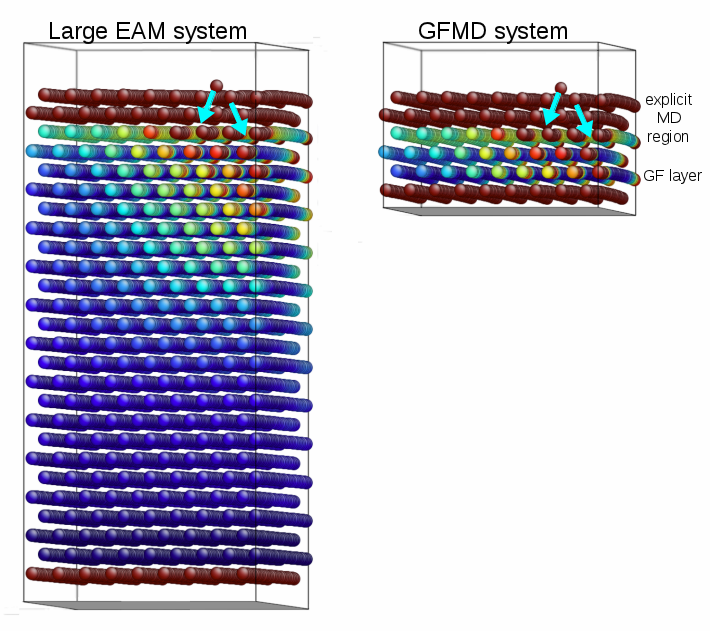
The microstructure of many materials is essentially disordered, meaning that there are a large number of small-scale structural elements which can be arranged in many possible ways.  For instance, common metals, such as aluminum and nickel, are composed of a jumble of crystalline grains.  Atoms within the crystalline grain are themselves ordered, but atoms at a grain boundary, where most deformation originates, occupy seemingly random positions.  The mechanics of these disordered materials is one of the most famous open problems in materials physics.

Machine learning algorithms can help cut through the structural complexity [1,2,3].  The local structure can be projected down from the high-dimensional configuration space to a subspace of a single dimension which is highly-correlated with the susceptibility of the local region to deform.  Then regions of weak structures can be readily identified so that the spatial distribution of weak spots can be connected to the origins of the material mechanical properties.  The machine learning method can also be reverse engineered to expose the attributes that contribute to the weakness of a region.  Furthermore, by looking for an Arrhenius relationship between temperature likelihood to deform, it is sometimes possible to identify the energy barrier associated with each small-scale deformation.

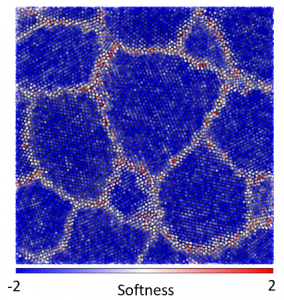
In previous work, I adapted and applied the above method, using a support vector machine, to study poly-crystalline materials.  Typically, defects (dislocations, vacancies, grain boundaries…) are said to control the mechanics of these materials, but the disordered regions within the core of the defects affects the mechanics of the defects themselves.  Our work demonstrated the dominant role of local structure in determining the weak spots within defects, even with realistic (delocalized) metallic bonding.  In this material, a lack of symmetry of the atomic environment was responsible for weakening an area of the material.  Contrary to expectations, though consistent with experimental measurements, the weak regions all had essentially the same energy barrier height preventing deformation.  The work helped illuminate the connection between disordered regions within poly-crystals and bulk glasses.

[1] Cubuk, Ekin Dogus, Samuel Stern Schoenholz, Jennifer M. Rieser, Brad Dean Malone, Joerg Rottler, Douglas J. Durian, Efthimios Kaxiras, and Andrea J. Liu. “Identifying structural flow defects in disordered solids using machine-learning methods.” Physical review letters 114, no. 10 (2015): 108001.

[2] Schoenholz, Samuel S., Ekin D. Cubuk, Daniel M. Sussman, Efthimios Kaxiras, and Andrea J. Liu. “A structural approach to relaxation in glassy liquids.” Nature Physics 12, no. 5 (2016): 469-471.

[3]  Sharp, Tristan A., Spencer Thomas, Ekin Dogus Cubuk, Samuel S. Schoenholz, David Srolovitz, Andrea J. Liu. “Using machine learning to extract atomic energy barriers in poly-crystalline materials.” Submitted 2017.  Accepted PNAS 2018.

Within biological tissues, cell shape may be indicative of the chemical and mechanical micro-environment.  Experiments on isotropic and homogeneous packings of cells, as shown below, connect the 3D shapes with tissue properties.  Unfortunately, quantitatively measuring 3D shapes of cells is burdensome, requiring high-quality confocal microscopy and image post-processing.  Another approach to quantifying 3D cell shapes uses 2D imagery without ever reconstructing 3D shapes.  Instead, cell-vertex models with quasi realistic geometry can be used to  generate mappings between 3D shapes of cells and the ensemble of 2D shapes seen in a single image.   Researchers may now trace cells in simple 2D imagery to determine the distribution of shapes, and compare them to the model to determine the ensemble of 3D cell shapes.

We are working to release a software package to provide these 3D shape estimates from traces of 2D cells.  This method has allowed us to compare predictions from the 3D cell vertex model with experimental measurements.

Molecular dynamics (MD) simulations can require large amounts of computer time and memory.  This is especially true in simulations of solid lattices of atoms, since elastic strains extend long distances and capturing the effects can require millions or billions of atoms.  The GFMD method is a mathematically and conceptually elegant simulation technique that can dramatically help.

GFMD stands for Greens Function Molecular Dynamics.  The method uses a function called the static surface Greens function (GF) of the material.  The concept will be described more in the next paragraph.  Importantly, the GF essentially contains all the information about the linear behavior of the lattice without having to simulate the lattice.  What it means is that regions of the atomic lattice with small strains can be deleted from the simulation, and the single layer of atoms at the boundary of the region can be controlled in a more complicated way.  Being able to discard those large regions of the lattice means that the simulation reaps large savings in memory and CPU time.

Campañá and Müser [1] introduced GFMD and showed how the method can be naturally used in molecular dynamics.  Our first paper rigorously developed GFMD based on the atomic interactions of lattice of molecules, making it an elegant and seamless boundary for MD simulations [2].   Our second paper (in preprint) extends GFMD to realistic, many-body interactions between atoms–which can be very slow and benefit the most from the speed-up [3].

To give an idea of the technical underpinning, we describe a few more details of the method.  The idea is that, as long as the strain is small, the atomic interactions can be considered at linear order.  In simulations of friction, for instance, large plastic strains occur near the surface of a solid, where a full, explicit, MD simulation must be used.  But further away from the surface, the Hamiltonian of the system can be approximated to quadratic order in the atomic positions.

The first and second derivatives of the Hamiltonian compose the external forces and dynamical matrix of the atoms, and, given that the atoms form a regular crystalline structure, transfer function methods may be used to calculate the GF.  The surface GF is nothing other than the equilibrium displacements of the surface atoms when the surface is subject to a point force.  Given the linearized Hamiltonian, the effect of an arbitrary exerted force on the surface is given by the the super-position of the GF displacements.

For many-body potentials, complications arise.  False forces are generated, so called ghost forces, at the layer of atoms that connects the explicit region from the linearized substrate.  Also, the forces cannot be decomposed into having a single-atom source, complicating implementation into standard MD codes. Meticulous attention to the formalism and familiarity with MD codes allowed us to introduce the appropriate domain decomposition, into explicit, substrate, and GFMD layers.

This detailed work results in a dramatically faster code. The plot at the top of this post indicates the speed up from running GFMD as opposed to the full system. The time per simulation time step scales with system size as rather than . Furthermore, the system is comprised of far fewer atoms, and so energy minimization requires fewer time steps.

[1] Campañá, Carlos, and Martin H. Müser. “Practical Green’s function approach to the simulation of elastic semi-infinite solids.” Physical Review B 74.7 (2006): 075420. https://journals.aps.org/prb/abstract/10.1103/PhysRevB.74.075420

[2] Pastewka, Lars, Tristan A. Sharp, and Mark O. Robbins. “Seamless elastic boundaries for atomistic calculations.” Physical Review B 86.7 (2012): 075459.  https://journals.aps.org/prb/abstract/10.1103/PhysRevB.86.075459

[3] Sharp, Tristan A., Lars Pastewka, and Mark O. Robbins. “Green’s function molecular dynamics with multi-body interactions.” In preparation (preprint available upon request).