tribology – T. A. Sharp

Molecular dynamics (MD) simulations can require large amounts of computer time and memory. This is especially true in simulations of solid lattices of atoms, since elastic strains extend long distances and capturing the effects can require millions or billions of atoms. The GFMD method is a mathematically and conceptually elegant simulation technique that can dramatically help.

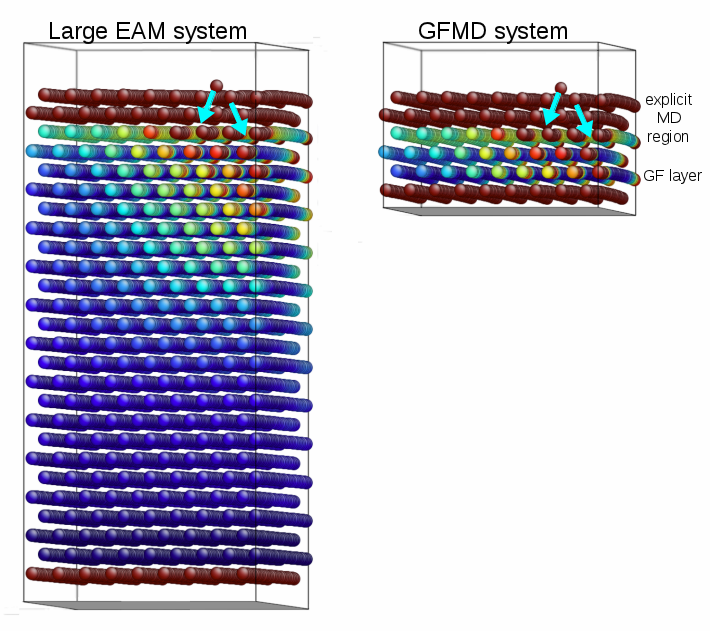
GFMD stands for Greens Function Molecular Dynamics. The method uses a function called the static surface Greens function (GF) of the material. The concept will be described more in the next paragraph. Importantly, the GF essentially contains all the information about the linear behavior of the lattice without having to simulate the lattice. What it means is that regions of the atomic lattice with small strains can be deleted from the simulation, and the single layer of atoms at the boundary of the region can be controlled in a more complicated way. Being able to discard those large regions of the lattice means that the simulation reaps large savings in memory and CPU time.

Campañá and Müser [1] introduced GFMD and showed how the method can be naturally used in molecular dynamics. Our first paper rigorously developed GFMD based on the atomic interactions of lattice of molecules, making it an elegant and seamless boundary for MD simulations [2]. Our second paper (in preprint) extends GFMD to realistic, many-body interactions between atoms–which can be very slow and benefit the most from the speed-up [3].

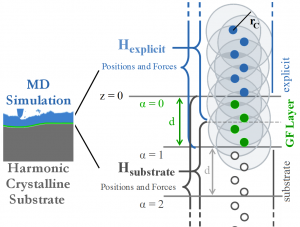
To give an idea of the technical underpinning, we describe a few more details of the method. The idea is that, as long as the strain is small, the atomic interactions can be considered at linear order. In simulations of friction, for instance, large plastic strains occur near the surface of a solid, where a full, explicit, MD simulation must be used. But further away from the surface, the Hamiltonian of the system can be approximated to quadratic order in the atomic positions.

The first and second derivatives of the Hamiltonian compose the external forces and dynamical matrix of the atoms, and, given that the atoms form a regular crystalline structure, transfer function methods may be used to calculate the GF. The surface GF is nothing other than the equilibrium displacements of the surface atoms when the surface is subject to a point force. Given the linearized Hamiltonian, the effect of an arbitrary exerted force on the surface is given by the the super-position of the GF displacements.

For many-body potentials, complications arise. False forces are generated, so called ghost forces, at the layer of atoms that connects the explicit region from the linearized substrate. Also, the forces cannot be decomposed into having a single-atom source, complicating implementation into standard MD codes. Meticulous attention to the formalism and familiarity with MD codes allowed us to introduce the appropriate domain decomposition, into explicit, substrate, and GFMD layers.

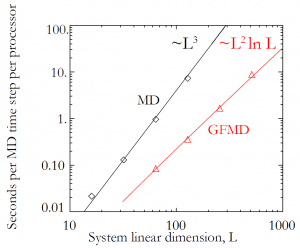
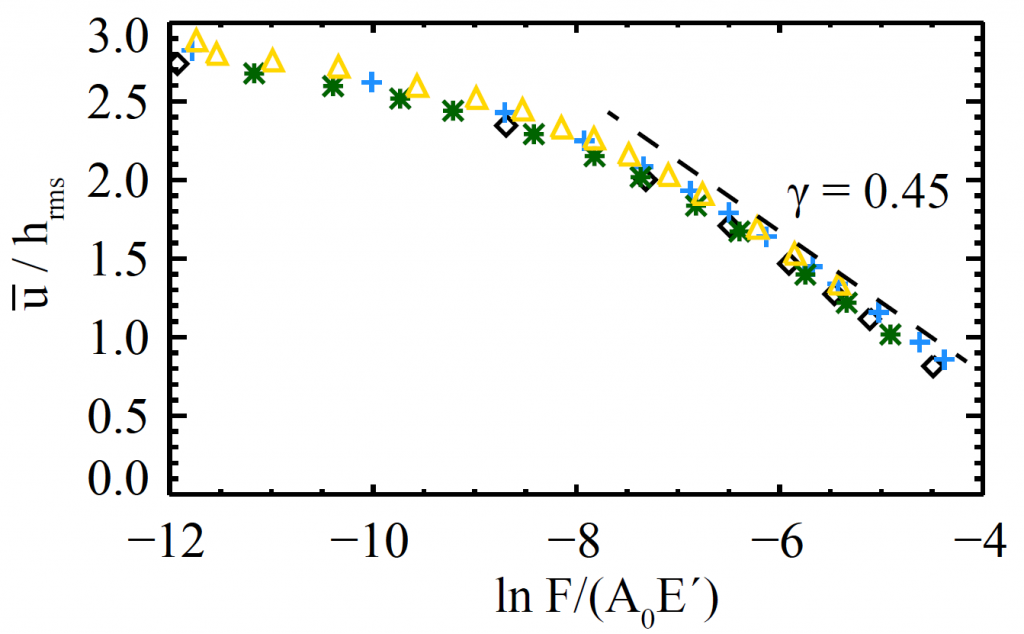
This detailed work results in a dramatically faster code. The plot at the top of this post indicates the speed up from running GFMD as opposed to the full system. The time per simulation time step scales with system size $L$ as $\mathcal{O}(L^2\ln{L})$ rather than $\mathcal{O}(L^3)$ . Furthermore, the system is comprised of far fewer atoms, and so energy minimization requires fewer time steps.

[1] Campañá, Carlos, and Martin H. Müser. “Practical Green’s function approach to the simulation of elastic semi-infinite solids.” Physical Review B 74.7 (2006): 075420. https://journals.aps.org/prb/abstract/10.1103/PhysRevB.74.075420

[2] Pastewka, Lars, Tristan A. Sharp, and Mark O. Robbins. “Seamless elastic boundaries for atomistic calculations.” Physical Review B 86.7 (2012): 075459. https://journals.aps.org/prb/abstract/10.1103/PhysRevB.86.075459

[3] Sharp, Tristan A., Lars Pastewka, and Mark O. Robbins. “Green’s function molecular dynamics with multi-body interactions.” In preparation (preprint available upon request).

Essentially all materials have rough surfaces at small scales. This can be a problem for engineers designing electrical contacts, thermal contacts, or seals to prevent leaks, since the roughness creates gaps between the two contacting surfaces. By increasing the pressure, the two solids can be forced closer together, reducing the gaps somewhat, but some space between the surfaces usually still remains.

Two blocks in compression may appear to be in full contact, but there is nearly always microscopic roughness that leads to gaps. For randomly-rough geometries, only $\nabla h_{rms}$ , the root-mean-squared slope of the surface, determines the microscopic contact area, for an applied force on the block, $F_N$ , made of material with Young’s modulus $E$ .

Two blocks in compression may appear to be in full contact, but there is nearly always microscopic roughness that leads to gaps. For randomly-rough geometries, only $\nabla h_{rms}$ , the root-mean-squared slope of the surface, determines the microscopic contact area, for an applied force on the block, $F_N$ , made of material with Young’s modulus $E$ .

Work with Mark O. Robbins quantified how surprisingly resilient the gaps are, and how important they are in determining the contact properties. To analyze the problem, we had to overcome technical challenges related to the large range of length scales of random-rough geometry on typical material surfaces, usually millimeters down to atomic scales. The rough geometry can be modeled using the mathematics of random (self-affine) fractals. Large-scale parallel processing on a computing cluster is required to simulate and analyze contact between many random realizations of rough 3D cubes of length 1000 atoms on a side. We worked with Lars Pastewka to write C++ code for GPUs to do fast simulations using lattice Greens functions and continuum-elastic Greens functions, which will be described in a later post.

Small example region of contact at the atomic scale for two similar surfaces, a bent lattice and a stepped lattice. If the material can yield, stepped surfaces produce more plasticity and lead to increased contact area (dark atoms). The amount of increase is given by $\nabla h_{rms}$ . However, $\nabla h_{rms}$ must be very large to enter the limiting plastic regime, where the contact area is the applied force over the material yield stress.

We found that the large-scale features of the material’s surface get flattened more easily, but the small-scale roughness cannot be squeezed away even at considerable pressures; we found that the fraction of the surface that is in contact is well-defined and at common pressures is less than 20%. Within this regime the fractional contact area obeys a simple law: $f_A \approx \kappa \hspace{1mm} p/ (E' \nabla h_{rms})$ , where $p$ is the confining pressure, $E'=E/(1-\nu^2)$ is the material’s contact modulus, $\nu$ is the effective Poisson ratio, $E$ is the material’s Young’s modulus, and $\nabla h_{rms}$ is the root-mean-squared slope of the original roughness profile[1]. $\kappa$ is a dimensionless constant with value about 2.2.

Atoms on the surface of a solid are colored red if they experience a repulsive force from the opposing surface. The statistical properties of the contact and pressure spatial distributions change with atomic scale features.

We considered this problem with both continuum-scale and atomic-scale simulations. We found that the continuum results can often be applied to small scales, meaning that continuum analyses are often appropriate for nanotechnology applications[2]. At the atomic-scale, the concept of contact area gets replaced by the number of atoms that exert repulsive forces on the other surface. However, for very rough or crystalline surfaces, atomic-scale plasticity causes the value of $\kappa$ in the above equation to increase, up to a value of 10.0. We went on to analyze the transition from elastic to plastic contact with roughness.

The gap (here quantified by the mean surface separation $\bar{u}$ ) approaches zero as the log of applied force $F$ . When $\bar{u}$ is normalized by surface rms height $h_{rms}$ and $F$ is normalized by the product of macroscopic contact area and contact modulus, $A_0 E'$ , the result collapse for different symbols, corresponding to continuum and atomistic simulations with varying roughness parameters. The lowest forces correspond to effects from our simulations having limited size, while the regime with slope $\gamma$ corresponds to an exponential relationship between applied pressure and the gap size.

The gap (here quantified by the mean surface separation $\bar{u}$ ) approaches zero as the log of applied force $F$ . When $\bar{u}$ is normalized by surface rms height $h_{rms}$ and $F$ is normalized by the product of macroscopic contact area and contact modulus, $A_0 E'$ , the result collapse for different symbols, corresponding to continuum and atomistic simulations with varying roughness parameters. The lowest forces correspond to effects from our simulations having limited size, while the regime with slope $\gamma$ corresponds to an exponential relationship between applied pressure and the gap size.

Even if the contacting materials are very stiff, they can seem much less so because of the gap from roughness at the contacting surface; the rough topography can be compressed more easily than the solid material. For both atomic and continuum analyses, the average gap width, $\bar{u}$ decreases slowly with force. We quantified this and showed that at large confining force, $F$ , it follows $\bar{u} = -\gamma h_{rms} \text{ln(} F/A_0 E' \text{)}+ c$ where $h_{rms}$ is the root-mean-squared height of the original surface, $A_0$ is the apparent surface area. As a result, the stiffness of the interface is $k_I \approx 0.5 * F / h_{rms}$ . The stiffness of the interface is extremely low when there is no confining pressure, and so the surface roughness dominates the mechanical response of the whole two-block system.

References:
Chapter 5 of my thesis (papers in preparation)

Sampling of the related work that helped build up this picture:

 Hyun, S., et al. "Finite-element analysis of contact between elastic self-affine surfaces." Physical Review E 70.2 (2004): 026117.
 Pei, L., et al. "Finite element modeling of elasto-plastic contact between rough surfaces." Journal of the Mechanics and Physics of Solids 53.11 (2005): 2385-2409.
 Cheng, S. & Robbins, M.O. "Defining contact at the atomic scale."  Tribol Lett (2010) 39: 329. https://doi.org/10.1007/s11249-010-9682-5
 C Yang and B N J Persson 2008 J. Phys.: Condens. Matter 20 215214 http://iopscience.iop.org/article/10.1088/0953-8984/20/21/215214/
 Persson, B. N. J. "Relation between interfacial separation and load: a general theory of contact mechanics." Physical review letters 99.12 (2007): 125502.
 Mo, Yifei, Kevin T. Turner, and Izabela Szlufarska. "Friction laws at the nanoscale." Nature 457.7233 (2009): 1116.

T. A. Sharp

Category: tribology

Rigorous Greens functions for crystal surfaces

Contact properties of rough solids: all about the Gap