Mechanics of tissue

Models of biological tissues allow tissue stiffness to be connected with cell-level structure and processes. On short time scales, biological tissues have the mechanical properties of polymer networks embedded with cells and fluid. This is a complicated composite from a materials physics perspective. Experiments can study simplified tissues, with cells alone with no extracellular matrix, or of polymer networks with embedded cell-like particles. 

Simulation of polymer networks with disordered particle packings.

As part of the Physical Science of Oncology Center, I interact with Dr. Paul Janmey’s group and helped with several experiments within that lab.  The group extensively characterized the mechanics of tissues and found that applying moderate stress to tissues increases the modulus of the tissue by 200-300% in the direction orthogonal to the stress.

Polymer matrix serves many mechanical roles in a tissue. In addition to providing mechanical support itself, it can also prevent cells from rearranging on long time scales. Simulations can separate the two effects by choosing how the fibers are connected.

This behavior occurred also for simple tissues with polysaccharide beads embedded in collagen matrix.  Models demonstrated that the stiffening was completely inconsistent with polymer networks and simple jammed particles.  The network topology of the extra-cellular matrix helps determine these non-linear mechanical properties.  The models demonstrate the importance of small-scale plasticity in determining the viscoelastic properties of these materials.  I helped design new confocal microscopy experiments showed that small-scale plasticity did not occur in the tissues under the applied deformations.  New versions of the model On-going work aims to suppress small-scale plasticity in simple models of tissues to continue investigating the mechanical properties.

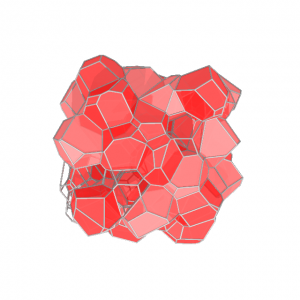
A 3D cell-vertex model based on the Voronoi tesselation can be simulated and analyzed for its mechanical properties. These models mimic the mechanical behavior of some simple cell tissues.

To investigate, I generalized a well-known cell vertex model to three dimensions to investigate mechanical properties in tissues with semi-realistic geometry.  The model consists of a random Voronoi tessellation of a set of points which move in accordance with a standard, simple energy functional for each cell: E_{cell} = (A-A_0)^2 + (V-V_0)^2.  The energy functional indicates that each cell has a preferred surface area, A_0, and volume, V_0.  We first used the model to study simple tissues which are simply packings of cells, which I started in conjunction with the group of Dr. M. Lisa Manning.  Similar to the two-dimensional cell vertex model, I found that the model exhibits a rigidity transition, controlled by the ratio of input parameters p=A_0/V_0^{2/3}.  We find that when p<5.4, the material is a solid packing, able to support deformations and sustain stresses.  For p>5.4, the material is a fluid, and cells are able to flow past one another.

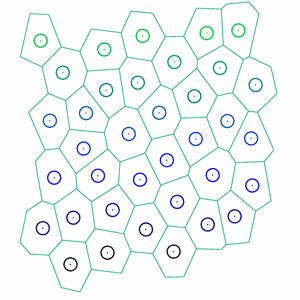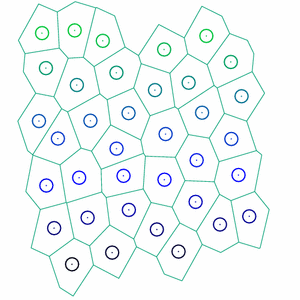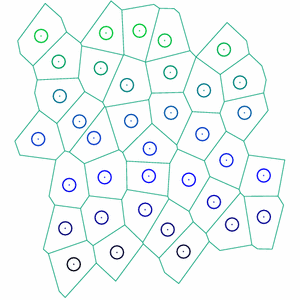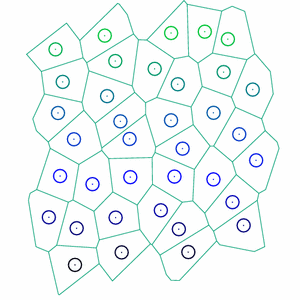
A cell vertex model under shear exhibits a range of non-linear responses. When p_0 is large, the tissue is fluid. Otherwise, the elastic moduli can vary by orders of magnitude depending on the stresses applied to the system.

On-going work aims to use the geometry from the cell vertex model to analyze tissue mechanical behavior, including viscoelasticity, using the three-dimensional cell vertex model with minimal enhancements to replicate the mechanics viewed in shear rheology experiments. Idealized models have an ever-growing role in biological physics.  Here, they provide insights into the microscopic processes that lead to non-linear tissue mechanics.

Go back

Your message has been sent