T. A. Sharp

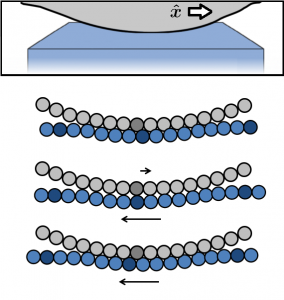
Friction between surfaces occurs at protrusions where the surfaces contact.  These protrusions are often modeled as spherical bumps on the surface, and for this reason, the prototypical model of friction is a sphere sliding on a flat surface.  Here, we use large simulations to find and explain new scaling of the friction force with asperity curvature [1].

On the atomic scale, the surfaces are composed of either crystalline or disordered material, and the materials may also have loose molecules adsorbed to their surfaces.  In the simplest case, the two surfaces are crystalline and clean.  Furthermore, it is simplest if the crystalline surfaces are aligned (ie commensurate) and if the surfaces do not stick together (ie are non-adhesive).  The other situations are more complicated, though actually more common in every-day situations, and we analyze them in other work [2].  Here, we describe the friction in the simplest, cleanest case.

Most models of friction predict a friction coefficient, , with simple behavior.  The Cattaneo-Mindlin model [3] assumes that each element of contacting surface area contributes a frictional force proportional to its normal force, with proportionality , .  This leads to the standard friction behavior in introductory physics textbooks, where the friction force and the normal force being proportional to each other (Amonton’s Law):  (where is the macroscopic friction coefficient and simple equals ).  However, the atomic geometry leads to different behavior for these surfaces.

The effect of atomic geometry for this system had been considered before [4,5,6].  However, those previous studies used interactions characteristic of adhesive surfaces (tested in [2]), and did not simulate with atomic geometry.  In our large-scale simulations of non-adhesive crystalline sphere sliding, we found unexpected behavior.

Fundamentally, to understand static friction, one must find the ways in which energy barriers arise in the system that oppose sliding.  To understand kinetic friction, one must find the ways in which energy leaves the system.  The energy is determined by the small scale atomic geometry at the surface and the long-range elastic interactions of the two materials.

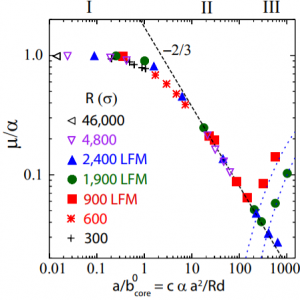
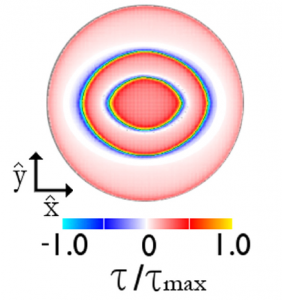
For the sphere sliding on a flat surface, elastic interactions distort the material during sliding in different ways depending on the amount of area in contact, leading to different values of the static friction coefficient.  Under a sphere, the contact area is a circle, and is the contact radius.  is compared to a pressure-dependent material property, , which is the core size of lattice dislocations at the interface between the two bodies.  We found three distinct regimes of elastic distortions, for small, medium, and large contact radii, each producing a different emergent friction, .

In regime I, the only elastic distortion comes from the sphere dragging the elastic substrate along the direction of motion.  The stress, , builds at all places in the contact uniformly from to the amount allowed by the local static friction uniformly, where is the local pressure.  As in the Cattaneo-Mindlin model, the friction coefficient is equal to its microscopic value, .

In regime II, stress builds primarily at the edges of the contact until a lattice dislocation develops and glides through the contact.  The nucleation instability undercuts the ability of the friction to raise to , and the newly-uncovered scaling can be derived.  In regime III, dislocations are arrested in the contact, and so the friction comes from the Peierls stress to move dislocations.  Surprisingly, the friction coefficient of a sphere of radius rises with contact area, since the Peierls stress rises with pressure.

This surprising result of non-monotonic friction in the simplest manifestation of the sliding asperity model shows that friction still hides many behaviors waiting to be unraveled.

[1] Sharp, Tristan A. et al. “Scale-and load-dependent friction in commensurate sphere-on-flat contacts.” Physical Review B 96.15 (2017): 155436. https://journals.aps.org/prb/abstract/10.1103/PhysRevB.96.155436

[2] Sharp, Tristan A. et al. “Elasticity limits structural superlubricity in large contacts.” Physical Review B 93 (2016):121402(R)  https://journals.aps.org/prb/abstract/10.1103/PhysRevB.93.121402

[3] Johnson, Kenneth. Contact mechanics. Cambridge university press, 1987.

Others’ work that helped build up this picture:
[4] Juan A. Hurtado and Kyung–Suk Kim.  “Scale effects in friction of single–asperity contacts. I. From concurrent slip to single–dislocation–assisted slip.” Proceedings of the Royal Society A (1999): 455 1989 http://rspa.royalsocietypublishing.org/content/455/1989/3363.short

[5] Juan A. Hurtado and Kyung–Suk Kim.  “Scale effects in friction of single–asperity contacts. II. Multiple–dislocation–cooperated slip” Proceedings of the Royal Society A (1999): 455 1989 http://rspa.royalsocietypublishing.org/content/455/1989/3363.short

[6] Gao, Yanfei. “A Peierls perspective on mechanisms of atomicfriction.” Journal of the Mechanics and Physics of Solids 58.12 (2010): 2023-2032. http://www.sciencedirect.com/science/article/pii/S0022509610001900

Molecular dynamics (MD) simulations can require large amounts of computer time and memory.  This is especially true in simulations of solid lattices of atoms, since elastic strains extend long distances and capturing the effects can require millions or billions of atoms.  The GFMD method is a mathematically and conceptually elegant simulation technique that can dramatically help.

GFMD stands for Greens Function Molecular Dynamics.  The method uses a function called the static surface Greens function (GF) of the material.  The concept will be described more in the next paragraph.  Importantly, the GF essentially contains all the information about the linear behavior of the lattice without having to simulate the lattice.  What it means is that regions of the atomic lattice with small strains can be deleted from the simulation, and the single layer of atoms at the boundary of the region can be controlled in a more complicated way.  Being able to discard those large regions of the lattice means that the simulation reaps large savings in memory and CPU time.

Campañá and Müser [1] introduced GFMD and showed how the method can be naturally used in molecular dynamics.  Our first paper rigorously developed GFMD based on the atomic interactions of lattice of molecules, making it an elegant and seamless boundary for MD simulations [2].   Our second paper (in preprint) extends GFMD to realistic, many-body interactions between atoms–which can be very slow and benefit the most from the speed-up [3].

To give an idea of the technical underpinning, we describe a few more details of the method.  The idea is that, as long as the strain is small, the atomic interactions can be considered at linear order.  In simulations of friction, for instance, large plastic strains occur near the surface of a solid, where a full, explicit, MD simulation must be used.  But further away from the surface, the Hamiltonian of the system can be approximated to quadratic order in the atomic positions.

The first and second derivatives of the Hamiltonian compose the external forces and dynamical matrix of the atoms, and, given that the atoms form a regular crystalline structure, transfer function methods may be used to calculate the GF.  The surface GF is nothing other than the equilibrium displacements of the surface atoms when the surface is subject to a point force.  Given the linearized Hamiltonian, the effect of an arbitrary exerted force on the surface is given by the the super-position of the GF displacements.

For many-body potentials, complications arise.  False forces are generated, so called ghost forces, at the layer of atoms that connects the explicit region from the linearized substrate.  Also, the forces cannot be decomposed into having a single-atom source, complicating implementation into standard MD codes. Meticulous attention to the formalism and familiarity with MD codes allowed us to introduce the appropriate domain decomposition, into explicit, substrate, and GFMD layers.

This detailed work results in a dramatically faster code. The plot at the top of this post indicates the speed up from running GFMD as opposed to the full system. The time per simulation time step scales with system size as rather than . Furthermore, the system is comprised of far fewer atoms, and so energy minimization requires fewer time steps.

[1] Campañá, Carlos, and Martin H. Müser. “Practical Green’s function approach to the simulation of elastic semi-infinite solids.” Physical Review B 74.7 (2006): 075420. https://journals.aps.org/prb/abstract/10.1103/PhysRevB.74.075420

[2] Pastewka, Lars, Tristan A. Sharp, and Mark O. Robbins. “Seamless elastic boundaries for atomistic calculations.” Physical Review B 86.7 (2012): 075459.  https://journals.aps.org/prb/abstract/10.1103/PhysRevB.86.075459

[3] Sharp, Tristan A., Lars Pastewka, and Mark O. Robbins. “Green’s function molecular dynamics with multi-body interactions.” In preparation (preprint available upon request).

The stiffness of a tissue reflects its cell-level properties. For instance, it is well known that increased stiffness can be an indicator a rapidly growing cancer in a tissue.  At UPenn, I am using simulations and theory, supported by experiments with the Penn Science of Oncology Center, to develop the biophysical understanding of tissue mechanics.

On short time scales, biological tissues have the mechanical properties of polymer networks embedded with cells and fluid. This is a complicated composite from a materials physics perspective. Experiments study simplified tissues, with cells alone with no extracellular matrix, or of polymer networks with embedded cell-like particles.  A long-term goal is to increase the utility of stiffness in characterizing the microscopic structure of the tissue.

Read more at this page.