T. A. Sharp

Contact properties of rough solids: all about the Gap

Essentially all materials have rough surfaces at small scales. This can be a problem for engineers designing electrical contacts, thermal contacts, or seals to prevent leaks, since the roughness creates gaps between the two contacting surfaces. By increasing the pressure, the two solids can be forced closer together, reducing the gaps somewhat, but some space between the surfaces usually still remains.

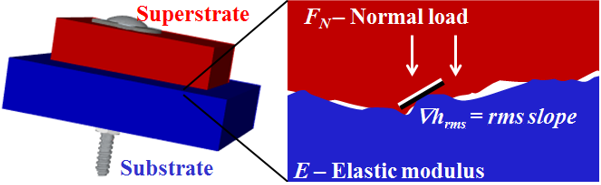
Two blocks in compression may appear to be in full contact, but there is nearly always microscopic roughness that leads to gaps. For randomly-rough geometries, only $\nabla h_{rms}$ , the root-mean-squared slope of the surface, determines the microscopic contact area, for an applied force on the block, $F_N$ , made of material with Young’s modulus $E$ .

Two blocks in compression may appear to be in full contact, but there is nearly always microscopic roughness that leads to gaps. For randomly-rough geometries, only $\nabla h_{rms}$ , the root-mean-squared slope of the surface, determines the microscopic contact area, for an applied force on the block, $F_N$ , made of material with Young’s modulus $E$ .

Work with Mark O. Robbins quantified how surprisingly resilient the gaps are, and how important they are in determining the contact properties. To analyze the problem, we had to overcome technical challenges related to the large range of length scales of random-rough geometry on typical material surfaces, usually millimeters down to atomic scales. The rough geometry can be modeled using the mathematics of random (self-affine) fractals. Large-scale parallel processing on a computing cluster is required to simulate and analyze contact between many random realizations of rough 3D cubes of length 1000 atoms on a side. We worked with Lars Pastewka to write C++ code for GPUs to do fast simulations using lattice Greens functions and continuum-elastic Greens functions, which will be described in a later post.

Small example region of contact at the atomic scale for two similar surfaces, a bent lattice and a stepped lattice. If the material can yield, stepped surfaces produce more plasticity and lead to increased contact area (dark atoms). The amount of increase is given by $\nabla h_{rms}$ . However, $\nabla h_{rms}$ must be very large to enter the limiting plastic regime, where the contact area is the applied force over the material yield stress.

We found that the large-scale features of the material’s surface get flattened more easily, but the small-scale roughness cannot be squeezed away even at considerable pressures; we found that the fraction of the surface that is in contact is well-defined and at common pressures is less than 20%. Within this regime the fractional contact area obeys a simple law: $f_A \approx \kappa \hspace{1mm} p/ (E' \nabla h_{rms})$ , where $p$ is the confining pressure, $E'=E/(1-\nu^2)$ is the material’s contact modulus, $\nu$ is the effective Poisson ratio, $E$ is the material’s Young’s modulus, and $\nabla h_{rms}$ is the root-mean-squared slope of the original roughness profile[1]. $\kappa$ is a dimensionless constant with value about 2.2.

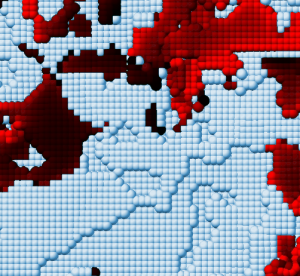
Atoms on the surface of a solid are colored red if they experience a repulsive force from the opposing surface. The statistical properties of the contact and pressure spatial distributions change with atomic scale features.

We considered this problem with both continuum-scale and atomic-scale simulations. We found that the continuum results can often be applied to small scales, meaning that continuum analyses are often appropriate for nanotechnology applications[2]. At the atomic-scale, the concept of contact area gets replaced by the number of atoms that exert repulsive forces on the other surface. However, for very rough or crystalline surfaces, atomic-scale plasticity causes the value of $\kappa$ in the above equation to increase, up to a value of 10.0. We went on to analyze the transition from elastic to plastic contact with roughness.

The gap (here quantified by the mean surface separation $\bar{u}$ ) approaches zero as the log of applied force $F$ . When $\bar{u}$ is normalized by surface rms height $h_{rms}$ and $F$ is normalized by the product of macroscopic contact area and contact modulus, $A_0 E'$ , the result collapse for different symbols, corresponding to continuum and atomistic simulations with varying roughness parameters. The lowest forces correspond to effects from our simulations having limited size, while the regime with slope $\gamma$ corresponds to an exponential relationship between applied pressure and the gap size.

The gap (here quantified by the mean surface separation $\bar{u}$ ) approaches zero as the log of applied force $F$ . When $\bar{u}$ is normalized by surface rms height $h_{rms}$ and $F$ is normalized by the product of macroscopic contact area and contact modulus, $A_0 E'$ , the result collapse for different symbols, corresponding to continuum and atomistic simulations with varying roughness parameters. The lowest forces correspond to effects from our simulations having limited size, while the regime with slope $\gamma$ corresponds to an exponential relationship between applied pressure and the gap size.

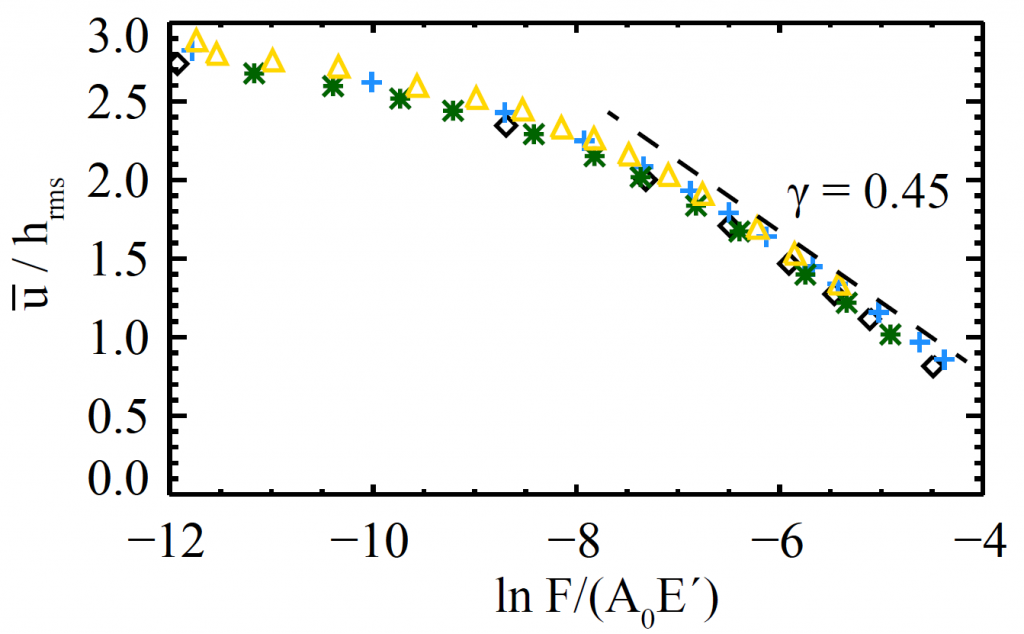
Even if the contacting materials are very stiff, they can seem much less so because of the gap from roughness at the contacting surface; the rough topography can be compressed more easily than the solid material. For both atomic and continuum analyses, the average gap width, $\bar{u}$ decreases slowly with force. We quantified this and showed that at large confining force, $F$ , it follows $\bar{u} = -\gamma h_{rms} \text{ln(} F/A_0 E' \text{)}+ c$ where $h_{rms}$ is the root-mean-squared height of the original surface, $A_0$ is the apparent surface area. As a result, the stiffness of the interface is $k_I \approx 0.5 * F / h_{rms}$ . The stiffness of the interface is extremely low when there is no confining pressure, and so the surface roughness dominates the mechanical response of the whole two-block system.

References:
Chapter 5 of my thesis (papers in preparation)

Sampling of the related work that helped build up this picture:

 Hyun, S., et al. "Finite-element analysis of contact between elastic self-affine surfaces." Physical Review E 70.2 (2004): 026117.
 Pei, L., et al. "Finite element modeling of elasto-plastic contact between rough surfaces." Journal of the Mechanics and Physics of Solids 53.11 (2005): 2385-2409.
 Cheng, S. & Robbins, M.O. "Defining contact at the atomic scale."  Tribol Lett (2010) 39: 329. https://doi.org/10.1007/s11249-010-9682-5
 C Yang and B N J Persson 2008 J. Phys.: Condens. Matter 20 215214 http://iopscience.iop.org/article/10.1088/0953-8984/20/21/215214/
 Persson, B. N. J. "Relation between interfacial separation and load: a general theory of contact mechanics." Physical review letters 99.12 (2007): 125502.
 Mo, Yifei, Kevin T. Turner, and Izabela Szlufarska. "Friction laws at the nanoscale." Nature 457.7233 (2009): 1116.

Visualizing mathematical analysis

In this post, I’d like to muse about the visualizations that are used when thinking about math, and how they can become quite beautiful as well as useful

When adding $7+8$ , many people imagine stacking blocks and then see $5$ spilling over the $10$ mark. This visual thinking made the answer seem “obvious” after doing it many times. When doing calculus, simple picture tricks are taught less often. If confronted with $\int_0^1 x dx$ we might quickly follow the memorized rule (from the fundamental theorem of calculus) that you add $+1$ to the exponent and divide by that number. $\int_0^1 x dx = \frac{x^2}{2} |_0^1 = \frac{1}{2}-\frac{0}{2}=\frac{1}{2}$ . But one can also remember that integration finds the area under a curve. With a picture in mind like the one below, we know that the red line cuts the unit square into two parts, each with area $\frac{1}{2}$ . The visual understanding will sometimes be a useful tool.

This post is supposed to illustrate that visual thinking remains useful in more advanced math, especially mathematical analysis (real analysis, complex analysis, functional analysis, differential equations) which deals with objects you can imagine embedded in space (that is, with a metric). It’s just that the pictures become more and more rarely taught. That means it takes a motivated attitude and some patience, because often in classes you generally have to figure it out for yourself.

I’ve found that it is worth the effort. This post will give a couple of examples using partial differential equations (PDEs). PDEs are very useful in engineering disciplines, yet it is not often taught how to picture the solution.

For example, let’s consider Laplace’s equation.

$\Delta \phi (x,y,z) = \frac{\partial^2 \phi}{\partial x^2} + \frac{\partial^2 \phi}{\partial y^2} = 0$

In classical physics, the electrical potential $\phi$ satisfies Laplace’s equation in three dimensions everywhere in space that there is no electric charge.

Say we want to know the potential in a long square pipe (a square cylinder), and we are given boundary conditions that specify the potential of each of the four sides. We can visualize what this equation is saying. The equation is local and it says that at every point of the domain, the x-curvature of the potential must cancel with the y-curvature of the potential.

I picked some boundary conditions (parabolas on the ends and constants at the side) and plotted the solution for $\phi$ below using Wolfram Alpha.

00_0

We can visually check that the curvature in x and y are equal and opposite at every point. Note how the solution looks like a stretched membrane. That’s because a stretched membrane also follows also follows Laplace’s equation. The solution is essentially the simplest surface you can draw that will connect the boundaries. If you can picture gluing an elastic sheet to those boundaries, you can picture the solution to Laplace’s equation.

Quantum probability current

In the example of the Schrödinger equation, the rate of change of the Hilbert state vector is determined by the Hamiltonian operator.

$i \hbar \frac{\partial}{\partial t} \left| \Psi(t) \right> = H \left| \Psi(t) \right>$

Operators and state vectors are abstract and we are sometimes interested in the positions basis specifically, since let’s face it, space seems to be a dominant aspect of reality. For the 1-dimensional problem of a free particle in the position basis we get the partial differential equation:

$\frac{\partial \Psi(x,t)}{\partial t} = i \hbar /2m \frac{\partial^2 \Psi(x,t)}{\partial x^2}$

$\Psi(x,t)$ is a complex field, in the sense that it has both real and imaginary components, and we can… really imagine it. The equation can be decomposed into two equations, one for the real part and one for the complex part of $\Psi(x,t) = \psi(x,t) + i \phi(x,t)$ , and we can plot it using a polar plot at each value of x. Again, the equation is local and says that the curvature is what matters. Where the curvature of the real part is positive, the imaginary part will grow. Where the curvature of the imaginary part is positive, the real part will shrink. If initially the field looks like a plane wave $\Psi(x,0) = e^{ipx} = \cos(px) + i \sin(px)$ where $p$ is a constant, the equation is telling us the corkscrew will turn.

Animation created with Python and ImageMagick

Now for the last part of this example, let’s look at the probability current. Usually when this is taught it seems to be a terribly opaque abstract construct. The probability current $\bold{j}$ is essentially the quantity that, together with the probability $P(x,t) = \Psi^* \Psi$ , satisfies the continuity equation $\frac{\partial}{\partial t} P(x,t) + \nabla \cdot \bold{j} = 0$ when $\Psi$ follows the Schrödinger equation. In one dimension it is

$j(x,t) = \hbar / 2mi (\Psi^*(x,t) \frac{\partial \Psi(x,t)}{\partial x} - \Psi(x,t) \frac{\partial \Psi^*(x,t)}{\partial x})$

It is difficult to picture what this equation is telling us! And yet wiki pages and textbooks* everywhere just state it and move on, letting the student grapple with it in the problem set. Let us stubbornly pursue a better picture. Using the polar form of the complex quantity $\Psi = A(x) e^{i \theta(x)}$ and working through a little math we get an equation for the flow of that is much simpler to picture.

$j(x) /P(x) = \hbar/m \: \frac{d}{dx}\theta$

The fraction of probability leaving location x is simply the derivative of the phase. In three dimensions, $\frac{d}{dx}\theta \rightarrow \nabla \theta( \bold{x} )$ which is saying that the probability current is just “flowing uphill” of the phase. That’s what the phase of a wave function has always meant, in case, like me, you weren’t told. This simpler version gives insight that might even be useful to a new wave of physics students.

Using the example of the corkscrew above, simply stated, the angle $\theta$ of the corkscrew increases constantly to the right, so our equation tells us there is uniform probability current to the right.

Here are other relations that are useful for visualizing these single-particle dynamics. Here I use shorthand for the derivatives so $\frac{d}{dt} P \rightarrow \dot P$ and $\nabla \theta \rightarrow \theta'$ . In the following, ignore the constant factors of $2m/\hbar$ which could be swallowed into the definition of the phase. The phase at a point x will decrease if it is sloped and it will increase due to curvature of A $\dot \theta 2m/\hbar = (\frac{A''}{A} - \theta'^2)$ . Meanwhile the amplitude A at the point x decreases from phase curvature or from slopes $\frac{\dot A}{A} \frac{2m}{\hbar}= -2 \frac{A'}{A} \theta' - \theta''$ . The probability increases from amplitude curvature (“smoothing out humps”) and decreases wherever the phase is sloped $\dot P = \nabla \cdot \bold{j} = 2 A'' - 2 \theta'^2$ . Hope this helps you picture some quantum dynamics.

The point of this post is just some examples of looking at partial differential equations to get a feeling for what the solutions look like. Locality of a PDE is a powerful property, something that college students often don’t appreciate in the standard science/engineering curriculum. My intuition dramatically increased once I began writing numerical codes to solve PDEs.

So I encourage the new mathematical scientists and engineers out there, don’t be afraid to break down your math problem and visualize it! It is worth the effort.

*Nearly all textbooks I have found stop at the abstract form of the probablility current. I eventually found however that Sakurai Modern Quantum Mechanics 1994 contains the same simple equation for $\bold{j}$ as above.

The step from Quantum Mechanics to Quantum Field Theory

There are several things that can still be confusing about quantum field theory (QFT) even if one already knows quantum mechanics. For example, how does QFT relate to the single-particle Schrödinger equation? For one, a single particle wave function $\phi(\bold{x})$ is already a continuous field, but quantum field theory refers to more than single-particle quantum mechanics. Moreover, we know that two particles are described in quantum mechanics as a six-dimensional wavefunction, yet quantum field theory discusses quantum fields that permeate all of space, in only three dimensions. The purpose of this post is to briefly summarize the steps from single-body to many-body quantum mechanics, which clarifies these questions. We follow the canonical quantization method. The intended audience is someone familiar with quantum field theory calculations, but wanting a reminder of its meaning.

Our starting point is a familiarity with quantum mechanics. One knows from quantum mechanics that a $N$ -particle wavefunction is $3N$ -dimensional. For instance, for $N=3$ , the wavefunction is written in position basis as $\phi(\bold{x_1},\bold{x_2},\bold{x_3})$ where $\bold{x_1}$ is the 3-dimensional position of particle 1. Recall that, for two identical particles, only the phase of a wavefunction changes if two of the particles are permuted, and in fact we can accept as experimental fact that the wavefunction is either completely symmetric (bosons) or anti-symmetric (fermions) under permutation. Note that the wavefunction notation above makes reference to which particle is which, and so for identical particles there is extra, non-physical information in the above notation. In fact, the symmetry means that it has $1/N!$ fewer distinct points in its domain than expected (i.e. than $R^{3N}$ ). This suggests that there is actually a more elegant way to describe the state. The more efficient way is in the basis of occupation number, which does not distinguish which particle is occupying each 3D-location, only how much each position is occupied. This better basis for identical particles is called Fock space. The Fock space vector $\Psi(\bold{x})$ means that there is $\Psi(\bold{x})$ amplitude for particles being at 3D position $\bold{x}$ . Rather than position basis, these vectors are often written in wavevector basis, but for conceptualizing them at this point, we can remain in position space.

Now recall the mathematical usefulness of the creation and annihilation operators of the 1D simple harmonic oscillator in quantum mechanics, $a^\dagger_i$ and $a_i$ . These operators create or annihilate a particle in the state $i$ . That is, $a^\dagger_2 \lvert 0 0 0 ... \rangle= \lvert 0 1 0 ...\rangle$ adds one particle to the location $\bold{x}=\bold{x}_2$ . We can define the so-called field operators that create a particle in eigenstate $\lvert \bold{x} \rangle$ as $\Psi(\bold{x}) = \sum \phi^*_i(\bold{x}) a_i$ .

The Heisenberg representation of quantum mechanics moves the time-dependence of the wavefunction to the operators. Using that here we finally have arrived at quantum field theory. The fields described by quantum field theory are these fields of operators, $\Psi(\bold{x})$ . They’re defined on 3-dimensional space, since they operate on M-dimensional Fock-space where M is the number of orthogonal multi-particle states that span the available space. These operator fields are free to fluctuate in magnitude. The operators operate on the current state of the fields. The background state is time-independent, and so all dynamics is in the field operators. (While the operators are the interesting, evolving quantities, they must ultimately be applied to the state to refer to the state of the system.) Commutation relations enforce the underlying quantization of the single-particle wavefunctions.

So this is the object that is studied by quantum field theory. The next question is, what are the dynamics of these fields?

In classical field theories, often the field equations of motion are not derived from microscopic equations, but instead they come from reasoning about symmetries and conserved quantities. For example, the Navier-Stokes equations describing fluid flow are often derived by postulating a continuous field and conserving mass, momentum, and energy, independent of any atomic picture. However, there is also a more complicated, microscopic approach to deriving Navier-Stokes that starts from Boltzmann’s equation for particle motions and an assumed scattering kernel. The situation is the same in QFT. The equation of motion of the field operators can be derived (amazingly) from the single-particle Schrödinger equation, as long as there are no interactions between particles. In more complex cases, the approach is often to use the symmetries of the problem to determine the properties of the equation of motion. These procedures lead to the Klein-Gordon and Dirac equations for relativistic bosons and fermions.

This post comes out of discussions from the book Advanced Quantum Mechanics by Schwabl, Quantum Field Theory by Schwatrz, Wikipedia, and discussion with Zlatko T and Matt W.